Il sistema posizionale
Terminiamo la nostra carrellata sulla storia dell'uso dei numeri, prendendo in considerazione le cifre che usiamo oggi ed il metodo "posizionale" con il quale le combiniamo per scrivere i numeri. In cosa consiste il metodo posizionale?
La sua principale idea, come suggerisce il nome, è che i simboli usati per le cifre non abbiano un valore fisso: il loro valore dipende dalla loro posizione nella scrittura del numero. Ad esempio, quando scriviamo il numero 2372, che cosa intendiamo? Questa scrittura sta per:
"due migliaia, tre centinaia, sette decine e due unità",
e cioè per:
2.103 + 3.102 + 7.101+2.100
.
Il valore di ognuna delle cifre di 2372
dipende dalla sua posizione: il primo "2" vale duemila, mentre l'ultimo "2" vale
solo due (esattamente come le conchiglie nelle cordicelle di diverso colore che
abbiamo già visto).
Notiamo che invece nelle scritture additive il valore dei
simboli è fisso: ad esempio nella scrittura romana di 72 = LXXII , i due "X"
valgono sempre "10", indipendentemente dalla posizione.
 Fig. 1: Un manoscritto indiano del VI secolo. (Credit: Les nombres (Math93)) |
I primi esempi noti di una scrittura numerica
basata sui seguenti elementi:
risalgono al V secolo d.C. (nel trattato
indiano di cosmologia Lokavibhaga, 485
d.C.); questo metodo si diffuse piuttosto rapidamente in India e in
Indocina, come è confermato dai documenti che testimoniano l'uso di tale cifre per
eseguire i conti, già nel secolo successivo.
Nel 773, arrivò a Bagdad un'ambasciata indiana con un omaggio per il califfo
Mansour ed ai suoi saggi: il calcolo e le cifre.
Muhammad
ibn Musa al-Khuwârizmi scrisse il primo testo in lingua araba presentando
la numerazione indiana posizionale nel IX secolo (dal suo nome deriva la parola
"algoritmo").
Nel X secolo, il monaco francese
Gerbert d'Aurillac
apprese il nuovo metodo dai Mori di Spagna e iniziò a introdurlo in occidente,
specialmente dopo esser divenuto Papa nel 999, col nome di Silvestro II.
Le tracce di uso della numerazione indo-araba in Europa sono comunque scarse
fino al XIII secolo, quando il matematico pisano
Leonardo
Fibonacci (che aveva viaggiato molto fra gli arabi) scrisse il
Liber Abaci, che illustra il sistema
posizionale ed il suo uso, e che fu il testo che più contribuì alla
sua introduzione sistematica in Europa.
Clicca QUI per vedere un esempio dei
sistemi medioevali di moltiplicazione.
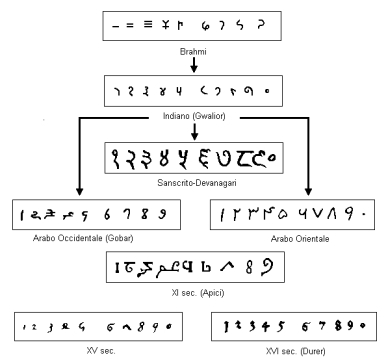 Fig. 2: La figura mostra alcuni passi dell'evoluzione dei simboli per le cifre Indo-Arabe. |
L'uso che facciamo tuttora delle cifre di origine indiana mostra la superiorità della scrittura posizionale rispetto a quella additiva romana (due ragioni fra tutte: la facilità nello scrivere numeri grandi e la possibilità di fare i conti usando le cifre scritte). Comunque il suo uso efficiente richiede una novità: avere una cifra per il numero zero.
La penetrazione del nuovo sistema in
Europa fu abbastanza lenta e all'inizio osteggiata; per esempio nel XIV secolo in
vari luoghi l'uso delle "cifre arabe" era proibito, temendo che fosse troppo
facile alterarle per eseguire truffe.
Ancora, nel Rinascimento si svolgevano
gare di calcolo fra "Abacisti" ed "Algoristi" (che usavano il calcolo scritto,
con le cifre indo-arabe) e l'abaco fu usato fino al XVIII
secolo.
Quanto sopra conclude questo breve trattato sullo sviluppo dei
sistemi di numerazione che ci ha portato a parlare dei cosidetti numeri naturali
(interi positivi più lo zero), mentre più lungo sarebbe il discorso se si
volesse considerare tutto ciò che l'uomo ha creato riguardo ai numeri. Alcuni
esempi? Lo sviluppo dei numeri frazionari, o di quelli negativi (quest'ultimi
risalenti ai tempi degli scribi egiziani), senza contare sviluppi più recenti,
come il completamento della formalizzazione rigorosa della teoria dei numeri
reali (ad es.
o
)
che avviene solo a metà del XIX secolo, o le più recenti e sofisticate teorie
dei numeri transfiniti o iperreali. Ma queste sono altre storie!