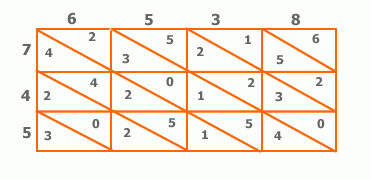
Vediamo uno degli antichi procedimenti di moltiplicazione, detto "per quadrettatura" o "per tavola", ad esempio nella moltiplicazione di 547 per 6538.

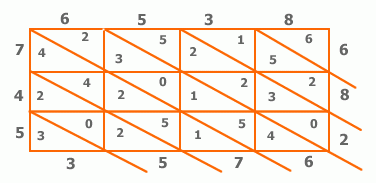
Riportate le cifre ai lati di una tabella come illustrato, si esegue in ogni casella (divisa in due da una linea diagonale) la moltiplicazione delle due cifre corrispondenti. A partire dal "6" in alto a destra, in ogni fascia diagonale si troveranno, rispettivamente, le cifre rappresentanti unità, decine, centinaia, e così via, del prodotto. Sommando lungo tale fasce troveremo quindi il risultato cercato  (3.576.286).

Questo metodo ci può sembrare molto lungo rispetto a quello da noi utilizzato oggi, ma allora era assolutamente più efficace di ogni calcolo sugli abaci, e permetteva una velocità nella moltiplicazione che i metodi precedenti l'uso delle cifre indiane non potevano uguagliare.