Quello che si può supporre è che, in effetti, l'umanità abbia elaborato la "capacità di conteggio" ben prima di possedere il concetto di numero. Perché diciamo ciò ed in che senso?

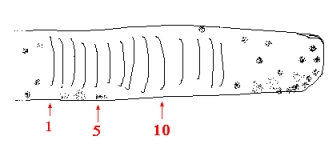
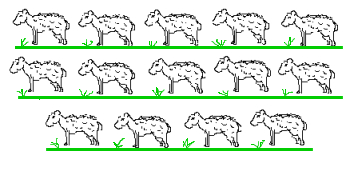
Come può ad esempio un pastore, totalmente analfabeta in aritmetica, controllare che il suo gregge di 14 pecore è tornato intatto dal pascolo all'ovile? Egli non ha alcun concetto di "14", però può semplicemente risolvere il suo problema così: il pastore prende un bastone e quando fa uscire le sue pecore dall'ovile, fa una tacca sul bastone per ogni pecora che esce. Al ritorno dovrà solo scorrere con un dito le tacche sul bastone, una per ogni pecora che rientra, e verificare così di non averne persa nessuna. 

Certo, ciò non gli dà la possibilità di dire "quante" pecore ha, ma questa procedura risolve il suo problema. La "pratica dell'intaglio" è stata, in effetti, in uso presso popolazioni di pastori fino in tempi relativamente recenti.
Il concetto fondamentale è quello di realizzare una corrispondenza biunivoca che sta proprio alla base del contare; in questo caso una corrispondenza fra le pecore e le tacche sul bastone. Naturalmente poco importa qual'è lo strumento di questa corrispondenza: il pastore potrebbe usare per il suo scopo un mucchietto di sassi (sempre uno per ogni pecora) e sarebbe la stessa cosa.

Possiamo figurarci analoghe situazioni di vario tipo: dei cacciatori arrivano presso un'altra tribù con un carico di 23 pelli, e le vogliono scambiare contro sacchi di mais e si accordano per scambiare due sacchi contro una pelle. 
Come effettueranno lo scambio senza saper contare (e tanto meno sommare o moltiplicare)?
Possono fare così: consegneranno le pellicce una ad una, ed in cambio di ognuna riceveranno i due sacchi di mais pattuiti, proseguendo fino all'esaurimento della merce. Nessuno dei partecipanti allo scambio saprà dire "quanti" oggetti sono stati dati e quanti ricevuti (le 23 pelli ed i 46 sacchi di mais), ma ognuno sarà sicuro che lo scambio è stato equo.

Un altro esempio è costituito dai rituali religiosi, come il recitare un certo numero di preghiere: il fedele non ha bisogno di saper contare se è munito di uno strumento adatto: una collana di preghiera (un "rosario" per i cattolici).

Fig. 1: Un rosario cristiano (a sinistra) e una collana di grani di preghiera islamica (a destra). Usate per recitare un certo numero fissato di preghiere, queste collane hanno tutte il medesimo principio: il fedele le "sgrana" con le mani enunciando per ogni grano la preghiera dovuta. Non c'è così bisogno di saper contare.

In questo stadio, "conteggio" significa sempre soltanto "stabilire una corrispondenza" fra gli oggetti da contare e degli "oggetti simbolo" (siano essi sassi, perline, conchiglie, tacche su ossa o bastoni, nodi su cordicelle o altro).

Perché parliamo di contare senza il numero? Perché a questo stadio non c'è il concetto di numero, ad esempio non ci sono nemmeno le parole per indicare i singoli numeri, nè tanto meno dei simboli; c'è solo la pratica del mettere in corrispondenza due insiemi di oggetti. 

Il successivo passo essenziale sarà di avere delle parole per i singoli numeri, e ciò avverrà in due stadi:

• Prima le parole che indicano i numeri saranno solo degli aggettivi: quando consideriamo "uno", "due" o "sei" come aggettivi numerali, essi sono solo attributi di insiemi, come nelle espressioni "due cani" o "sei barche". Qui "due" e "sei" hanno lo stesso valore di aggettivo, come "rosso" o "saporito". 
• Poi, con l'uso del numero come un vero e proprio nome (cioè un sostantivo) si ha il completo passaggio al concetto astratto di numero, infatti col passaggio al sostantivo si ha la possibilità di enunciare anche proprietà dei numeri stessi (e non solo degli oggetti contati), come quando, ad esempio, diciamo "il tre è dispari".