Dimostrazioni Automatiche
 Fig 1: HAL: l'intelligenza artificiale di 2001: Odissea nello spazio. |
e l'automazione delle dimostrazioni matematiche è un altro campo
applicativo in cui l'intelligenza artificiale ha raggiunto notevoli
risultati. La logica è uno degli strumenti più antichi, assestati e
rigorosi, utilizzati dall'uomo per formalizzare e spiegare il proprio
ragionamento. Per questo è utilizzata in intelligenza artificiale per
rappresentare la conoscenza su un problema, anche se questa scelta ha
delle limitazioni evidenti e non trova un consenso unanime. In riferimento all'architettura tipica dei sistemi di intelligenza artificiale, la base di conoscenza diventa in questo caso una collezione di asserzioni della logica dei predicati del primo ordine. Le regole di inferenza permettono di dedurre nuove asserzioni (teoremi) non esplicitamente contenute nella base di conoscenza iniziale.
Gran parte dei
programmi che utilizzano la logica in intelligenza artificiale sono
basati sugli studi sulla dimostrazione automatica di teoremi nella
logica, ed in particolare sul metodo di risoluzione messo a punto da
J.A. Robinson negli anni '60 ed allo sviluppo di strategie per rendere
più efficiente la dimostrazione. Figli di questi studi sono anche la
programmazione logica ed il linguaggio
Prolog (da PROgramming in LOGic)
in particolare, uno dei più interessanti ed innovativi paradigmi di
programmazione per lo sviluppo di applicazioni "intelligenti".
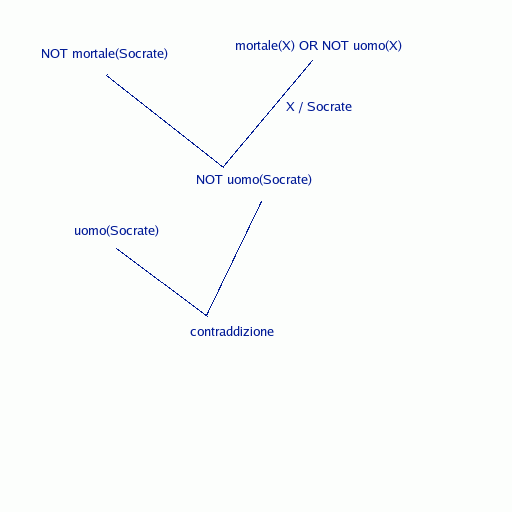
L'esempio seguente
riguarda una dimostrazione (analoga a quelle in linguaggio Prolog).
Data una base di conoscenza iniziale, si tratta di cercare di
dimostrare un 'teorema' (in realtà si tratta di un famoso sillogismo)
della filosofia antica: Socrate è mortale.
La base di conoscenza contiene le seguenti asserzioni:
- X è mortale oppure X non è un uomo (cioè: se X è un uomo, allora X è mortale)
- Socrate è un uomo
- mortale(X) OR NOT uomo(X)
- uomo(Socrate)
The Webweavers: Last modified Wed, 09 Mar 2005 11:04:58 GMT