Il calcolo della Unità Astronomica, ovvero della distanza che separa la Terra dal Sole, mediante le osservazioni dei transiti dei pianeti interni richiede l'applicazione di un metodo geometrico basato sulle misure dei tempi di transito presi da due punti diversi della superficie terrestre, lontani il più possibile secondo la direzione perpendicolare al piano dell'eclittica.

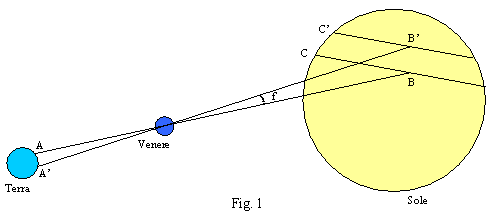
Un osservatore posto in A (fig. 1) vedrà il pianeta descrivere la corda C, mentre un osservatore posto in A' lo vedrà transitare sulla corda C', cosicché, ad uno stesso istante, Venere apparirà in due punti diversi, rispettivamente B e B'. La separazione angolare tra B e B' (angolo f) può essere ottenuta dalla differenza della durata del transito nei due luoghi di osservazione; d'altra parte la distanza tra i due punti A e A' è nota, così che è possibile risalire alla distanza BB' ed infine alla distanza Terra-Sole cercata.

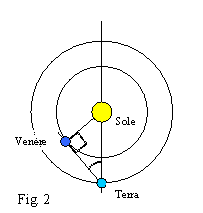
Cerchiamo ora di eseguire i calcoli utilizzando un metodo semplificato. L'elongazione massima di Venere - la sua distanza apparente dal Sole, vista dalla Terra - varia da 45° a 48°: per comodità, ipotizziamo orbite circolari e prendiamo il valore medio di elongazione massima di Venere, pari a 46° (fig. 2):

SV/ST = sen 46° = 0,72

da cui

SV = 0,72 x ST

ST = 1 UA

SV = 0,72 UA ;  TV = 0,28 UA

Sempre nell'assunzione di orbite circolari, cerchiamo di ricavare la velocità apparente di Venere. Il periodo sinodico di Venere ovvero il tempo che il pianeta, osservato dalla Terra, impiega per tornare in una stessa posizione rispetto al Sole, è di 584 giorni.

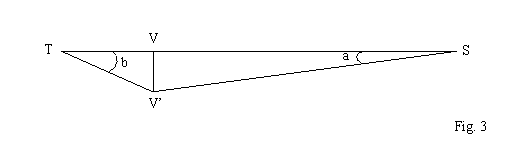
Nella figura 3:

    T = Terra

    S = Sole

    V = Venere in congiunzione inferiore

    V’ = Venere un’ora dopo la congiunzione

VV’ = TV x sen b = SV x sen a

sen b / sen a ≈ b/a = SV/TV = 0,72 / 0,28

L'angolo a descritto da Venere attorno al Sole in un'ora sarà (in primi d'arco):

a = 360 x 60 / 584 x 24

b = a x (0,72 / 0,28) = 360 x 60 x 0,72 / 584 x 24 x 0,28 = 4'

Dunque, la velocità con la quale Venere transita davanti al Sole è di circa 4 primi d'arco all'ora.

Tornando alla figura 1, supponiamo che AA' sia perpendicolare al piano dell'eclittica e che la distanza tra i due osservatori sia di 5.000 km. Ipotizziamo, inoltre, che il transito di Venere davanti al Sole duri 6 ore per l'osservatore posto in A' e 6 ore e 8 minuti per l'osservatore posto in A.

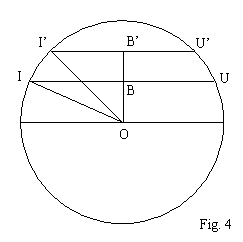
Nella figura 4 è rappresentato il disco solare con i due tracciati del transito I'U' e IU, osservati, rispettivamente, dalle due postazioni A' e A:

I'U' = 6h x 4'/h = 24'                        I'B' = 12'

IU = 6h 8m x 4'/h = 24,53'              IB = 12,27'

Il raggio del Sole sappiamo essere OI' = OI = 16', da cui, per il teorema di Pitagora:

BO = 10,269'  e  B'O = 10,583'

quindi

B'B = 0,314' = 0,00523°

Ma possiamo risalire anche alla misura in km di BB':

BB'/AA' = BV/AV = 0,72 UA / 0,28 UA

da cui

BB' = 72/28 x 5.000 km = 12.857 km

Quindi la distanza Terra-Sole, ovvero AB, risulterà:

sen 0,00523 / 2 x AB = 12.857 / 2

AB = 6.429 / sen 0,00262 = 140593346 km

che, considerando il raggio della Terra pari a 6378 km, corrisponde ad una parallasse solare di 9,36 secondi d'arco.

Si tratta, come abbiamo detto, di un metodo semplificato e, di conseguenza, il risultato che abbiamo ottenuto non rappresenta il valore corretto della distanza Terra-Sole. Le odierne misure dell'Unità Astronomica, realizzate con l'ausilio di satelliti e segnali radar, hanno portato al valore di 149.597.870 km, accettato dall'International Astronomical Union (IAU 1976); ma il valore calcolato da Newcomb nell'Ottocento, partendo dalle misure compiute in occasione dei transiti settecenteschi e secondo un metodo trigonometrico simile (ma più rigoroso) a quello esposto in queste pagine, non era molto diverso e, precisamente, di 149.668.465 km.