Il ricoprimento di una stanza qualsiasi non è che uno dei tanti (infiniti!) problemi per i quali non esistono (e non esisteranno) programmi che li risolvono.

Un esempio famoso viene dalla stessa informatica. Ci sono programmi che, per qualche motivo (spesso un errore di programmazione) "vanno in ciclo", cioè non terminano. Non è una bella situazione, perché noi siamo ad aspettare un risultato e non sappiamo se il calcolatore non risponde perché sta ancora calcolando (e magari ci risponderà nel prossimo secondo) o perché è in ciclo. Sarebbe bello (ed economicamente conveniente) se sapessimo decidere automaticamente e in modo generale se un certo programma può andare in ciclo.

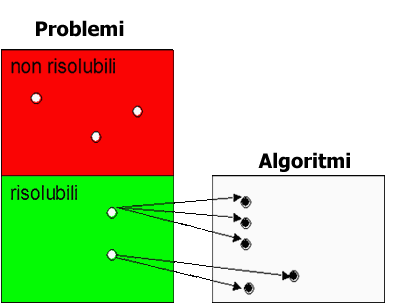
	Fig. 1: Problemi risolubili e irresolubili. I problemi sono partizionati in due classi (disgiunte): i problemi risolubili e quelli non risolubili. Ad ogni problema risolubile corrispondono gli algoritmi che lo risolvono (sono sempre più di uno, in realtà sono infiniti). Ai problemi non risolubili non corrisponde alcun algoritmo.

Ebbene, questo non si può fare, perché il seguente problema non è C-risolubile:

• Dati: un programma P e un dato "n" per P;
   
• Problema: stampare SI se P eseguito su "n" finisce l'esecuzione (dopo un certo tempo); stampare NO se P eseguito su n va in ciclo.

Osserva che non è possibile semplicemente provare ad eseguire P su n ed aspettare: questo basterebbe per rispondere SI (quando effettivamente l'esecuzione si ferma), ma quando rispondere NO? Anche dopo milioni di istruzioni eseguite, la terminazione potrebbe essere proprio l'effetto della prossima istruzione, come invece l'esecuzione potrebbe andare avanti all'infinito.

Il modo dei problemi è dunque suddiviso in due aree tra loro molto diverse: in una stanno i problemi C-risolubili, nell'altra quelli non C-risolubili (come i due problemi che abbiamo descritto qui: ricoprimento di una stanza qualsiasi e programmi che vanno in ciclo). Il seguente grafico rappresenta in modo sintetico il mondo dei problemi e delle loro soluzioni; osserva come ogni problema algoritmicamente risolubile abbia sempre più algoritmi risolutivi.  

Bibliografia

D. Harel. Computer a responsabilità limitata. Dove le macchine non riescono ad arrivare. Einaudi, Torino, 2002.